Besh, Big Data, Infraestructura
Nuestros compañeros de Data Science de Stratesys y en especial el experto Yaroslav Hernandez Potiomkin nos explica qué es el Big Data, cómo aplica a los diferentes departamentos de las empresas y qué diferencias existen entre los modelos paramétricos y no paramétricos.
Para profundizar más sobre estos temas, puedes contactar con los expertos.
Actualmente estamos experimentando una revolución del dato, lo que se traduce en mayor capacidad de almacenaje, mayor volumen y por ende, en mayor variedad de datos a causa de las nuevas herramientas, tecnologías y canales de comunicación como redes sociales, webs y apps. Además de, la velocidad y el procesamiento de datos relacionado con procesos de generación del dato y restricciones del modelo de negocio.
Estos tres conceptos, Volumen, Variedad y Velocidad definen el término “Big data”. Asimismo, en el caso de que esta definición pueda ser aplicada e integrada en los procesos de negocio, quiere decir que eventualmente podría haber la necesidad de un procesamiento y/o análisis de datos masivo.
Este término se aplica e integra en los procesos de negocio, por lo que nace la necesidad de un procesamiento y/o análisis de datos masivo.
Muchas empresas están convencidas de que la analítica avanzada puede potencialmente mejorar sus procesos de negocio relacionados con logística, marketing, operaciones y estrategia.
A menudo, estos procesos están cubiertos por técnicas de modelado de datos y metodologías como el motor principal de los Sistemas de Soporte a la Decisión (DSS). Los DSS permiten descubrir conocimiento valioso escondido en los datos y que reflejan el estado del negocio y su tendencia, siempre teniendo en cuenta la información histórica.
De esta manera, la toma de decisión asistida es mucho más efectiva que únicamente el conocimiento, la experiencia y la intuición.
Diferencias entre Modelo Paramétrico y Modelo No-Paramétrico en la estructura Big Data
Centrándonos en la parte más técnica, existen muchas herramientas y soluciones relacionadas con “Big data” y analítica avanzada en general. Los problemas del mundo real son muy complejos y es muy importante elegir una técnica apropiada o incluso, diseñar una metodología personalizada.
Principalmente, existen dos tipos de modelos: paramétricos y no-paramétricos.
En el modelo paramétrico, los datos siguen una distribución de probabilidad con un conjunto fijo de parámetros. Esto es muy interesante porque las hipótesis iniciales se cumplen y, además, desde el punto de vista teórico, el modelo está bien fundamentado.
Podrían surgir dificultades, por ejemplo, cuando existe comportamiento multimodal en los datos, lo que implica que muchos modelos como Quadratic Discriminant Analysis (QDA) or Linear Discriminant Analysis (LDA) (Hastie et al. 2008) no sean apropiados y que las posibles inferencias realizadas sean erróneas. Pero, por ejemplo, Fisher Linear Discriminant Analysis (FLDA) (Hastie et al. 2008) no requiere la asunción de normalidad, ni tampoco Principal Component Analysis (PCA) (Jolliffe, I.T. 2013).
Los modelos no-paramétricos se pueden diferenciar en:
1) Métodos no vinculados a una distribución en concreto, modelos como: kNN, PCA, Árboles de Decisión
2) Métodos sin una estructura predefinida: Support Vector Machines (SVM) y Non-parametric Local Polynomial Regression.
En el caso de SVM, está muy claro que el número de parámetros crece con el volumen de datos ya que el número de vectores soporte está acotado por el número de observaciones.
Por otro lado, a diferencia de modelos de regresión parámetricos con Linear predictor function en los que la relación entre las variables independientes y dependientes está predefinida, la regresión no-paramétrica proporciona un marco más flexible porque la asunción de linealidad y la forma del predictor function se relajan, aunque los errores aún deben ser i.i.d. Nótese que la linealidad siempre se refiere a los parámetros, no a los datos.
Esto quedará reflejado en el siguiente ejemplo de Pagan and Ullah, 1999 donde se coge el logaritmo del salario en términos de la edad de los varones canadienses con el nivel educativo medio en el 1971.
La relación se asume cuadrática en edad. Entonces, la fórmula del modelo lineal paramétrico sería como sigue:
Nótese que este modelo es aún lineal respecto los parámetros.
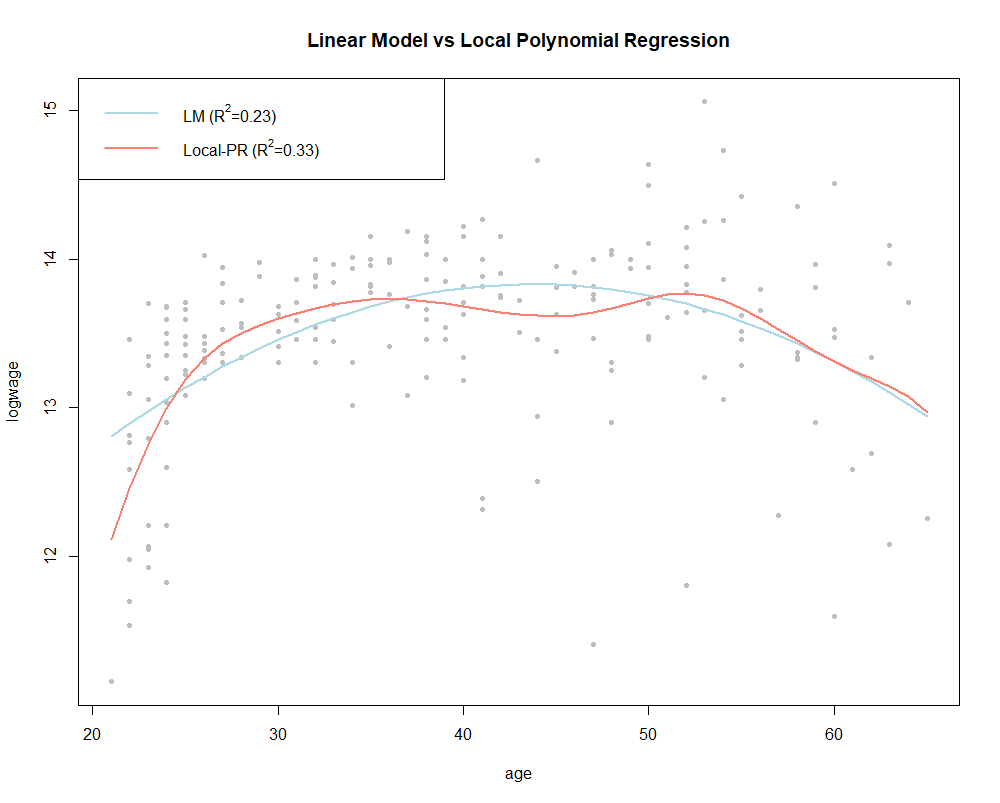 En la Fig. 2 se muestra el ajuste de la regresión paramétrica versus el modelo no-paramétrico.
En la Fig. 2 se muestra el ajuste de la regresión paramétrica versus el modelo no-paramétrico.
Para el modelo no-paramétrico, el parámetro bandwidth se estima por cros-validación usando el criterio AIC. De hecho, en el modelado no-parámetrico, a diferencia de modelos paramétricos lineales, a menudo es conveniente no asumir homocedasticidad y estimar la varianza condicional. El siguiente código R se utilizó para generar el ejemplo práctico:
library(“np”)
data(“cps71”)
model.par <- lm(logwage ~ age + I(age^2), data = cps71)
summary(model.par)
model.np <- npreg(logwage ~ age, regtype = “ll”, bwmethod = “cv.aic”, gradients = TRUE, data = cps71)
summary(model.np)
plot(cps71$age, cps71$logwage, type=”o”, ylab=”logwage”, xlab=”age”, main=”Linear Model vs Local Polynomial Regression”)
lines(cps71$age, model.par$fitted.values, col=”lightblue”, lwd=2)
lines(cps71$age, fitted(model.np), col=”salmon”, lwd=2)
legend(“topleft”, legend = c(expression(paste(“LM (“, R^2, “=0.23)”)), expression(paste(“Local-PR (“, R^2, “=0.33)”))), col=c(“lightblue”, “salmon”), lwd=2)








Deja un comentario