Validación de modelos en el análisis de datos estadísticos

Yaroslav Hernández Potiomkin, Data Scientist, nos propone una explicación sobre la validación de modelos en el análisis de datos estadísticos. Este tipo de validaciones son comúnmente usadas en Azure. Si necesitas ampliar conocimiento o resolver dudas no dudes en contactarnos.

 Validación de modelos. Buena Praxis

En el análisis de datos estadístico existen muchas aplicaciones y, por ello, hay muchas maneras de validar el modelo. La mayoría de las veces dependerá de lo que queramos medir para determinar la bondad del modelo. Comunmente, a este conjunto de criterios se le llama Bondad de Ajuste o en inglés Goodness of Fit (GoF). Además, estas medidas no sólo evalúan la potencia de predicción del modelo, sino que también permiten validar las hipótesis iniciales. Tener en cuenta las hipótesis iniciales del modelo es lo primero en lo que se fija un Data Scientist. La implicación lógica “Hipótesis –> Tesis” significa que para una hipótesis que no se cumple, la tesis puede o no cumplirse. Esto significa que podemos obtener un resultado absolutamente inesperado y, por tanto, no nos podemos fiar de las estimaciones del modelo en cuestión. A nivel industrial y empresarial esto se traduce en la robustez de las soluciones y riesgo de tomar decisiones basadas en estimaciones posiblemente erróneas.

Criterios de la bondad de ajuste

En Modelos Lineales Generalizados o GLM (P. McCullagh and J.A. Nelder, 1989), lineales siempre respecto los parámetros, se utiliza la medida de scaled deviance (P. McCullagh and J.A. Nelder, 1989; Paul E. Johnson, 2016) que coincide con la formulación del ratio de verosimilitud (para Likelihood Ratio Test, LRT). En el caso de datos continuos y con la asunción de normalidad, scaled deviance deriva en la suma de cuadrados de los residuos normalizada por la varianza (parte residual no reducible, sigma cuadrado). En el caso de la Binomial (clasificación), scaled deviance toma otra forma, en concreto, aplicando un factor multiplicativo, deriva en comunmente conocida función de error llamada cross-entropy. La medida de scaled deviance se utiliza principalmente para modelos anidados. El coeficiente de determinación múltiple (R2) (González J.A., Cobo E., Muñoz P., Martí M, 2008), se define justamente como

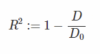
D es deviance y D0 es null deviance (en este caso el denominador de scaled deviance, es decir, el término de normalización, se cancelaría, por ello deviance y scaled deviance sería de uso equivalente en esta definición). El null deviance representa el modelo de benchmark, el modelo donde no se utilizan predictoras y asimismo corresponde a la suma de cuadrados total (para datos continuos). Luego está el R2 adjusted, que es lo mismo que el R2 pero con penalización por el número de parámetros. Otro criterio muy interesante es el PRESS (Allen, D. M., 1974; D. C. Montgomery, E. A. Peck, 1992), que permite calcular la potencia predictiva del modelo correspondiente al muestreo LOO (leave one out), pero sin hacer la cros-validación. El cálculo de PRESS implica los residuos y los coeficientes h (los conocidos como leverage y que indican el peso de cada observación o dato en el modelo). También se puede aproximar el R2 con PRESS. Acabamos de ver diferentes funciones de la bondad de ajuste y la relación entre ellas.

Criterios de potencia predictiva

Los siguientes métodos no están relacionados con ningún modelo en particular ni asunciones iniciales, como por ejemplo la familia de distribuciones exponencial o la homosedasticidad. Simplemente, nos fijamos en el tipo de la variable respuesta y aplicamos una función que mide la desviación entre la estimación y la realidad. En algunas ocasiones esta función coincidirá con la función error que naturalmente derivaría del modelo que se está utilizando y las restricciones aplicadas, pero no tiene por qué.

Por ejemplo, en el caso de respuesta continua existe NRMSE (Normalized Root Mean Square Error) donde el denominador puede ser la media, un intervalo, una cota superior, etc. A veces es conveniente usar el error absoluto en vez del cuadrático, cuando por ejemplo el objetivo es maximizar la distancia entre vectores de forma uniforme (en el espacio multi-dimensional). Incluso, dependiendo del problema, interesa usar el sumatorio absoluto en vez del promedio o ponderación. Otra medida muy fácil de interpretar es el error relativo (absoluto o con signo), aunque tiene varios inconvenientes. MAPE sería el promedio del error relativo absoluto. A menudo se usan percentiles del error, en vez del promedio, ya que dan una noción de estabilidad. Existen otros indicadores de diferentes ámbitos de aplicación (Y. Hernandez-Potiomkin, M. Saifuzzaman, E. Bert, R. Mena Yedra, T. Djukic, J. Casas, 2018).

Para datos categóricos, tenemos combinaciones de TP (true positive), TN (true negative), FP (false positive) y FN (false negative). Sobre estos indicadores se pueden construir muchas medidas de ajuste: precision, recall, F-measure y otras muchas combinaciones. Una forma de resumir o contraponer estas medidas es construir una grafica donde cada eje represente uno de estos indicadores. La curva ROC (Receiver Operating Characteristic) representa el FP y TP. Cada punto en el espacio 2-D es un clasificador y la envolvente convexa (ROCCH) (T. Fawcett, 2006) de los puntos da la curva ROC que representa tanto clasificadores plausibles como puntos que forman dicha envolvente. La recta con la pendiente 1 y la ordenada de origen 0 representa respuesta aleatoria. Los puntos por debajo de esa recta son clasificadores sub-óptimos.

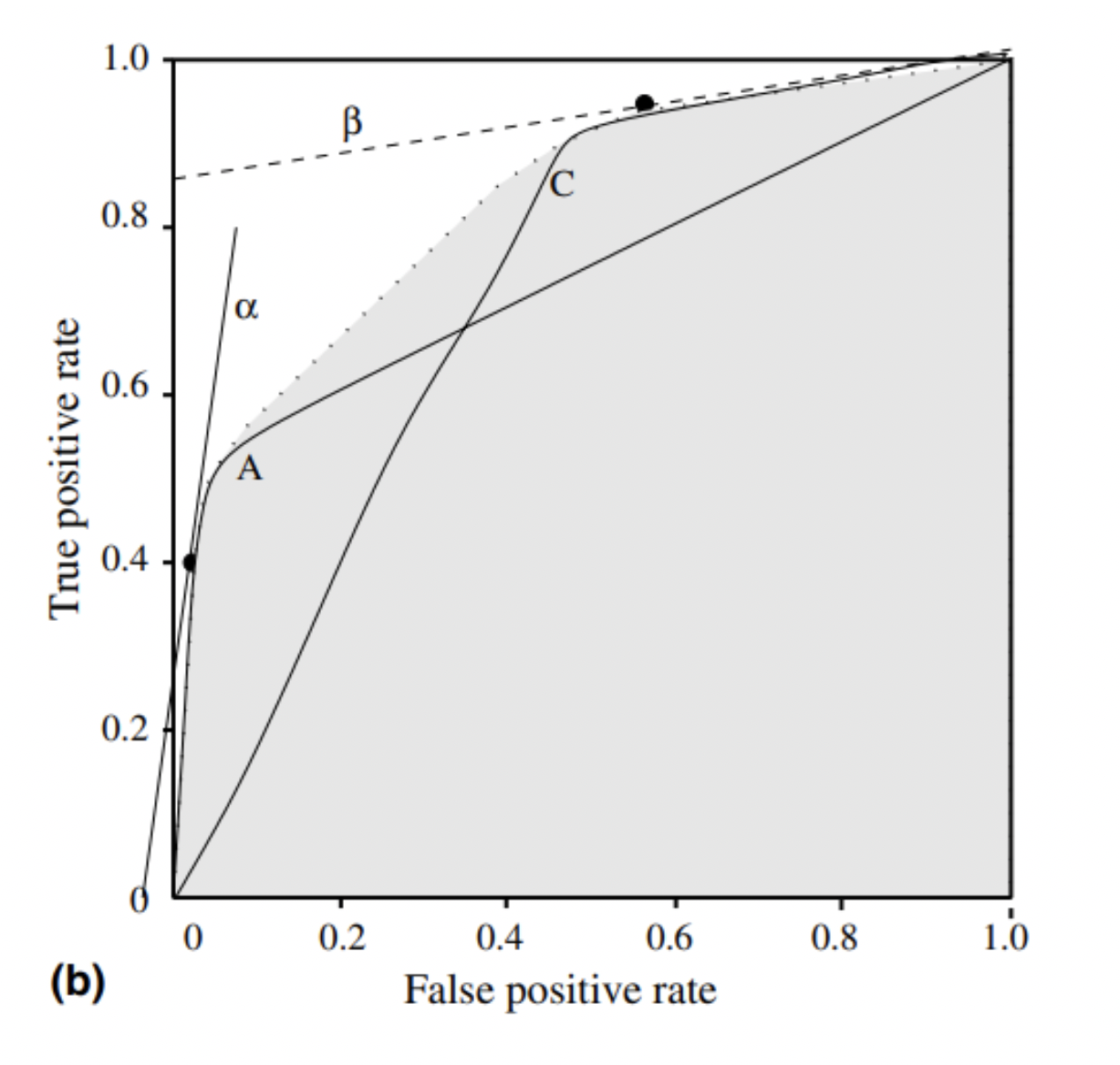
Fig. 1: Envolventes convexas ROC (ROCCH) de dos conjuntos de clasificadores.

Esta gráfica da una idea del umbral de clasificación a elegir dependiendo del problema que se intenta resolver. Se puede calcular coste versus beneficio utilizando los valores de TP y FP que corresponden a cada clasificador (umbral de decisión). En la Fig. 1 se puede ver cómo las diferentes pendientes representan escenarios distintos según caso de uso.

Otra medida que se utiliza mucho por ejemplo en el Procesado de Lenguaje Natural es la perplexity (D. Jurafsky and J. H. Martin, 2019):

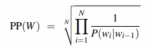
En este caso la fórmula corresponde al modelo 2-gramas. Es la inversa de la probabilidad del test set, normalizada por la longitud de la secuencia. Cuanto menor es este indicador, mayor es la probabilidad de observar una secuencia determinada de palabras (del conjunto de test). Los parámetros de la fórmula de la perplexity varía según el modelo, pero la forma y el concepto son los mismos.

Se han presentado varios procedimientos de validación de modelos y medidas de la bondad de ajuste y potencia predictiva. Se han proporcionado ejemplos y casos de uso para dichas medidas e indicadores. Este conjunto de herramientas ayudan a medir factores que no son directamente observables. Por ello, hay que tener en cuenta el sesgo que puede ser introducido a la hora de realizar dichas mediciones. Por ejemplo, la forma de particionar los datos en conjuntos de aprendizaje y validación, a menudo no basta con hacer una partición aleatoria. Esto sucede con frecuencia en modelos para marketing, en los cuales el comportamiento de clientes tiene un lapso de tiempo y va asociado a unas acciones. Esta secuencia temporal se debe respetar a la hora de particionar datos y solamente introducir la aleatoriedad para tomar muestras.